Correct answer: 2 π−−√ in. Explanation: The surface area formula for a sphere is: A = 4πr2, where r is the sphere's radius. Substitute the given value for the sphere's area into the equation and solve for r to find the radius: 8 = 4πr2. 2 π = r2. r = 2 π−−√ in.. Free Sphere Radius & Diameter Calculator - calculate sphere radius, diameter step by step
Rearrange formula for volume of a sphere for radius YouTube
Question Video Finding the Equation of a Sphere given the Coordinates of Its Centre Nagwa
Ex Equation of a Sphere Given the Center and Radius YouTube
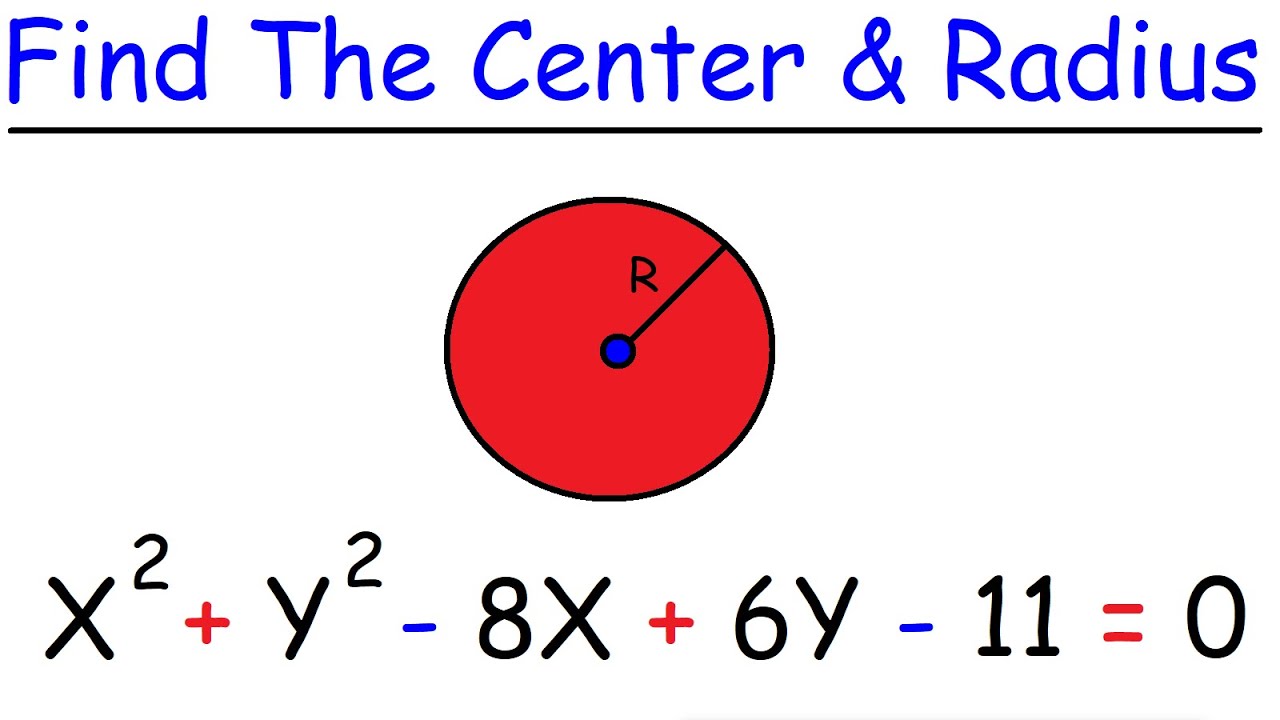
How To Find The Center and Radius of a Circle YouTube
![How can we Write the Equation of a Sphere in Standard Form? [Solved]](https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/how-to-write-the-equation-of-a-sphere-in-standard-form-01-1-1620197466.png "How can we Write the Equation of a Sphere in Standard Form? [Solved]")
How can we Write the Equation of a Sphere in Standard Form? [Solved]
Volume And Surface Area of A Sphere When Given Diameter YouTube
Area of Circle Definition, Formula & Examples ChiliMath
What Is The Formula To Find The Volume Of A Sphere? Rettig Thedidismind
The Best Way to Find the Radius of a Sphere wikiHow
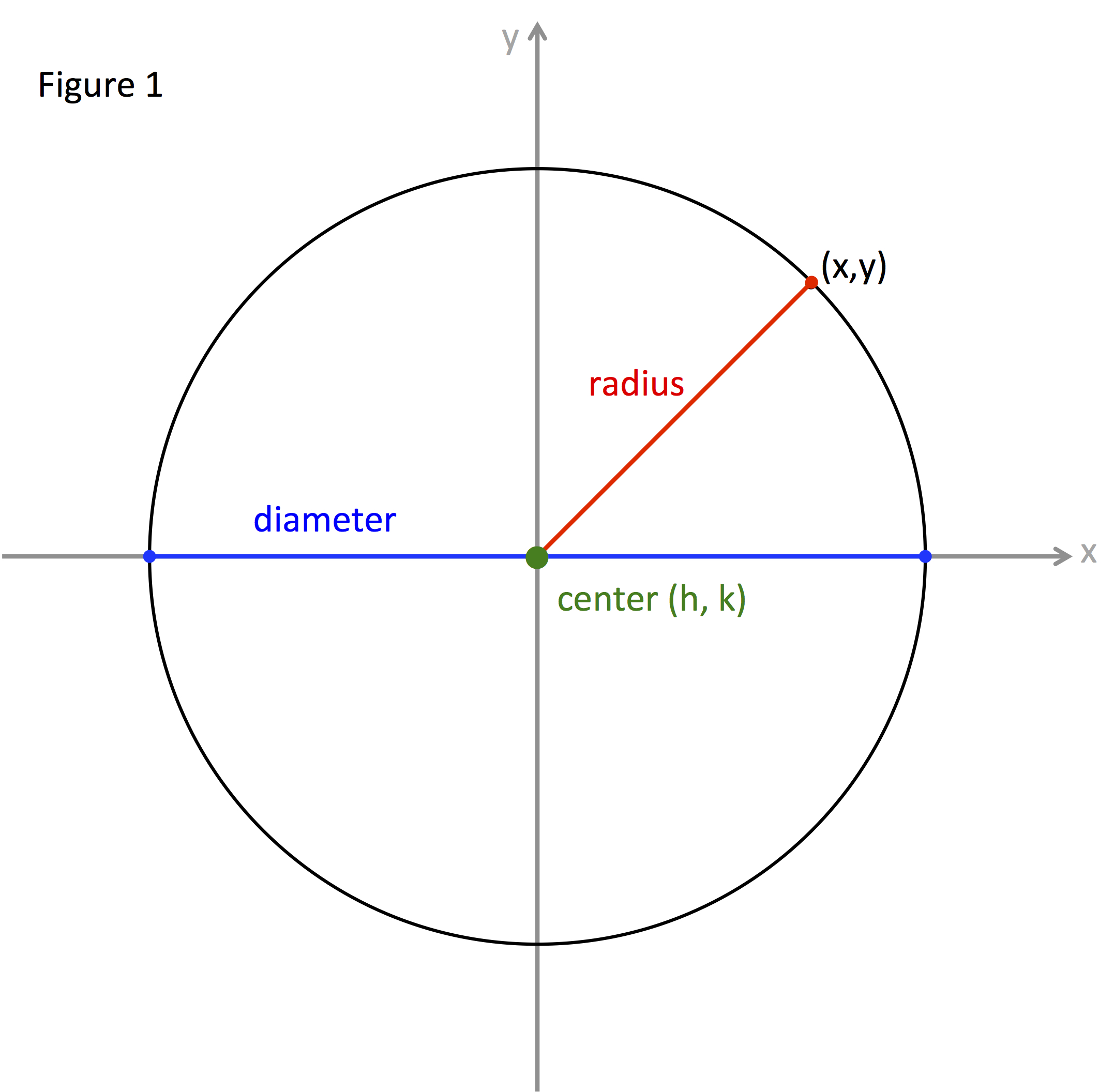
Circle CenterRadius Equation
Ex 11.2, 6 Find radius of a sphere whose surface area Ex 11.2
8.3 Finding Radius of a Sphere YouTube
Sphere Volume Formula Math Animation YouTube
How to find Radius and centre of the sphere Analytic Geometry problem YouTube
How To Find The Equation of a Sphere, Center, & Radius Given The Endpoints of its Diameter YouTube
The Best Way to Find the Radius of a Sphere Wiki How To English
Equation of Sphere YouTube
Volume of Sphere with Radius YouTube
Finding the Radius Formula & Concept Video & Lesson Transcript
5 Ways to Calculate the Radius of a Circle wikiHow
Mathematics. The purpose of tis program is to calculate the center and radius of a sphere given its general equation. Also, it displays a graph so that the user can have and idea of how it would look like in 3D.. Answer. We know that the standard form of the equation of a sphere is ( 𝑥 − 𝑎) + ( 𝑦 − 𝑏) + ( 𝑧 − 𝑐) = 𝑟, where ( 𝑎, 𝑏, 𝑐) is the center and 𝑟 is the length of the radius. We need to rearrange the given equation into this form. First, we add 289 to both sides of the equation to give us ( 𝑥 + 5) + ( 𝑦.
